Are you up for the 100 Problem Challenge?
These are optional (and very challenging) math questions that students at BEAM Discovery (rising 7th graders) work together to solve.
Try out this (slight variation) on a question BEAM students solved last summer. (Answer below the problem.)
PROBLEM:
A pirate ship with a crew of 34 half-rate pirates captured a measly booty of 34 doubloons (pirate money). To avoid a mutiny the captain divided the money evenly, giving everyone (including herself) exactly one doubloon to start off.
The captain can make a proposal to redistribute doubloons, but more pirates must vote in favor than vote against for it to take effect, and the captain does not even get a vote! (Other crew members can choose not to vote at all, which is called abstaining.)
If the captain proposes a new way to distribute the 34 doubloons, then the crew takes a vote. Pirates will always vote in favor if it means they get more doubloons after the vote. Pirates will always vote against if it means they lose some of their doubloons. Pirates whose share of the booty doesn’t change will abstain. For a vote to pass, it must have more pirates voting in favor than against. The total of all of the booty must always be 34, and all shares must be integers (0 or greater). However, the scheming captain can redistribute the booty many times: she might make one proposal, then another, then another, changing each pirate's share multiple times.
What is the most doubloons the captain can acquire?
Scroll down for the answer.
Solution:
Let’s first consider a few scenarios to understand how the voting and passing of proposals work.
Example of a proposal that wouldn’t pass: Suppose the captain proposes that 2 pirates plus herself receive doubloons from 3 other pirates, and every other pirate keeps their single doubloon. This would not pass since 3 pirates would vote against (those who lost their doubloon), 2 pirates would vote for (remember the captain doesn’t get a vote!), and every other pirate would abstain. Thus, the proposal fails 3-2.
Example of a proposal that would pass: Now suppose the captain instead proposes that 2 pirates plus herself give doubloons to 3 other pirates, while every other pirate stays the same. Then this proposal would pass 3-2 since 3 pirates receive more doubloons while only 2 non-captain pirates lose doubloons.
Now that we understand how voting works a bit better, a couple questions come to mind:
Can the captain get all 34 doubloons?
Is it even possible for the captain to get two doubloons?
And finally, is there an algorithmic way the captain can get more and more doubloons?
To try to get as many doubloons as possible, the captain might think of proposing that she and 16 other pirates receive a doubloon from each of the other 17 pirates:
But this proposal would fail 17-16. After some thought, it doesn’t seem like the captain can get any doubloons no matter how arrr-dously she try, which leads to step 1.
STEP 1:
The captain arrr-rives at the conclusion that she must give away her doubloon and arrr-gues to her shipmates that it’s best for everyone for half of them (including herself) to give their doubloon to another pirate.
STEP 2:
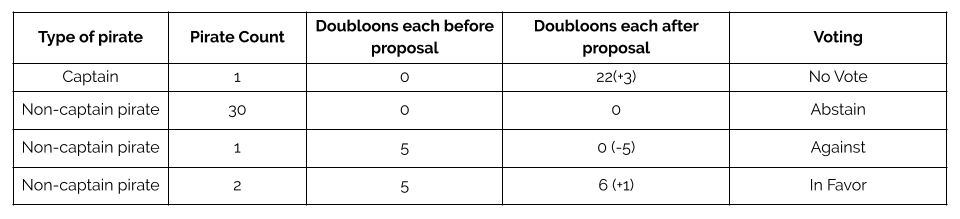
Now this captain realizes that a pirate will vote in favor whenever they gain doubloons no matter how many, and will vote against no matter how many they lose. So she can take all the doubloons away from pirates with many and just give one each to just enough to outvote them. She proposes that of the 17 pirates with doubloons, a little under half will get just one more doubloon, while a little under half will lose all their doubloons! Of course, she will receive all the extras. The 16 landlubbers without doubloons will still have nothing.
Scheming, the captain realizes that with each proposal she can take almost half of the remaining booty for herself, using half + 1 of the crews’ doubloons to pay off the crew who still have doubloons to lose. So, she goes on in this fashion for 3 more votes (see Steps 3-5), until she, the first mate, and the second mate are the only ones with any doubloons (see Step 6).
STEP 3:
STEP 4:
STEP 5:
STEP 6:
Up until now, the captain had kept the first mate and second mate happy by promising them more and more doubloons with every vote, but with one final proposal she turns the table on them, taking the dozen doubloons they have between the two of them and giving 3 of them away to secure the vote. She makes off with a tidy 31 doubloons and 3 loyal (short-sighted) crew members. The remaining 30 pirates are left scratching their heads over how they gave away all their loot.
Some questions to ponder
Can you do even better than this scalawag of a captain? Would her strategy have worked if they had captured 66 gold coins instead, or 130 treasure chests? Is there anything special about the number 34 (or 66 or 130)?