... And Now for Some (Pirate) Math

Are you up for the 100 Problem Challenge? 

These are optional (and very challenging) math questions that students at BEAM Discovery (rising 7th graders) work together to solve.

Try out this (slight variation) on a question BEAM students solved last summer. (Answer below the problem.)

PROBLEM:

A pirate ship with a crew of 34 half-rate pirates captured a measly booty of 34 doubloons (pirate money). To avoid a mutiny the captain divided the money evenly, giving everyone (including herself) exactly one doubloon to start off.

The captain can make a proposal to redistribute doubloons, but more pirates must vote in favor than vote against for it to take effect, and the captain does not even get a vote! (Other crew members can choose not to vote at all, which is called abstaining.)

If the captain proposes a new way to distribute the 34 doubloons, then the crew takes a vote. Pirates will always vote in favor if it means they get more doubloons after the vote. Pirates will always vote against if it means they lose some of their doubloons. Pirates whose share of the booty doesn’t change will abstain. For a vote to pass, it must have more pirates voting in favor than against. The total of all of the booty must always be 34, and all shares must be integers (0 or greater). However, the scheming captain can redistribute the booty many times: she might make one proposal, then another, then another, changing each pirate's share multiple times.

What is the most doubloons the captain can acquire?

Scroll down for the answer.

---

Solution:

Let’s first consider a few scenarios to understand how the voting and passing of proposals work.

Example of a proposal that wouldn’t pass: Suppose the captain proposes that 2 pirates plus herself receive doubloons from 3 other pirates, and every other pirate keeps their single doubloon. This would not pass since 3 pirates would vote against (those who lost their doubloon), 2 pirates would vote for (remember the captain doesn’t get a vote!), and every other pirate would abstain. Thus, the proposal fails 3-2.

Example of a proposal that would pass: Now suppose the captain instead proposes that 2 pirates plus herself give doubloons to 3 other pirates, while every other pirate stays the same. Then this proposal would pass 3-2 since 3 pirates receive more doubloons while only 2 non-captain pirates lose doubloons.

Now that we understand how voting works a bit better, a couple questions come to mind:

• Can the captain get all 34 doubloons?

• Is it even possible for the captain to get two doubloons?

• And finally, is there an algorithmic way the captain can get more and more doubloons?

To try to get as many doubloons as possible, the captain might think of proposing that she and 16 other pirates receive a doubloon from each of the other 17 pirates:

But this proposal would fail 17-16. After some thought, it doesn’t seem like the captain can get any doubloons no matter how arrr-dously she try, which leads to step 1.

STEP 1:

The captain arrr-rives at the conclusion that she must give away her doubloon and arrr-gues to her shipmates that it’s best for everyone for half of them (including herself) to give their doubloon to another pirate.

STEP 2:

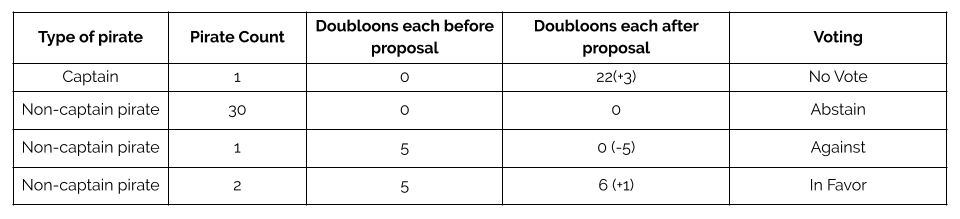
Now this captain realizes that a pirate will vote in favor whenever they gain doubloons no matter how many, and will vote against no matter how many they lose. So she can take all the doubloons away from pirates with many and just give one each to just enough to outvote them. She proposes that of the 17 pirates with doubloons, a little under half will get just one more doubloon, while a little under half will lose all their doubloons! Of course, she will receive all the extras. The 16 landlubbers without doubloons will still have nothing.

Scheming, the captain realizes that with each proposal she can take almost half of the remaining booty for herself, using half + 1 of the crews’ doubloons to pay off the crew who still have doubloons to lose. So, she goes on in this fashion for 3 more votes (see Steps 3-5), until she, the first mate, and the second mate are the only ones with any doubloons (see Step 6).

STEP 3:

STEP 4:

STEP 5:

STEP 6:

Up until now, the captain had kept the first mate and second mate happy by promising them more and more doubloons with every vote, but with one final proposal she turns the table on them, taking the dozen doubloons they have between the two of them and giving 3 of them away to secure the vote. She makes off with a tidy 31 doubloons and 3 loyal (short-sighted) crew members. The remaining 30 pirates are left scratching their heads over how they gave away all their loot.

Some questions to ponder

Can you do even better than this scalawag of a captain? Would her strategy have worked if they had captured 66 gold coins instead, or 130 treasure chests? Is there anything special about the number 34 (or 66 or 130)?

Announcing BEAM NYC High School Results!

In New York City, every 8th grader in the public school system must apply to go to high school.

The application process is incredibly important because the high school a student attends is one of the biggest predictors of their future opportunities. Yet it is also incredibly difficult for many students, particularly those from disadvantaged communities and under-resourced middle schools, who must often figure things out largely on their own.

BEAM is there to help them bridge that gap.

BEAM helps eighth graders navigate the whole process, from personalized guidance on finding strong-fit schools, to information sessions and interview preparation.

Now the exciting part: BEAM 8th graders have received their admissions results!

Overall, 51% of BEAM students earned spots at high schools that BEAM rates as Tier 1. An additional 18% were offered seats at Tier 2 schools, and 21% earned spots at Trusted schools. In total, 90% of BEAM students earned spots at schools that BEAM rates as Trusted or higher.*

These results demonstrate achievement far outside of typical outcomes for underserved students in New York City.

*BEAM rates NYC high schools as Tier 1 (offers calculus and greater than 85% of students who begin in 9th grade graduate prepared for college), Tier 2 (good course offerings and greater than 70% of graduates are prepared for college courses), or Trusted (good support and acceptable course offerings). Of 400 public high schools in NYC, only about 40 qualify as Tier 1 by these metrics. All Tier 1 schools are highly selective for admissions, and many Tier 2 schools are, as well. Tier 1 schools include specialized high schools, like Brooklyn Technical High School, and early college programs, like Bard High School Early College.

Here’s a complete list of high schools admissions for BEAM students to date:**

• Bard High School Early College (10)

• The Beacon School (4)

• Manhattan Center for Science and Mathematics (9)

• Manhattan/Hunter Science High School (2)

• University Heights High School (5)

• Benjamin Banneker Academy

• Midwood High School (4)

• Young Women's Leadership School

• Central Park East High School (2)

• East Side Community School

• Academy of American Studies

• Aviation Career & Technical Education High School (4)

• Bedford Academy

• Frank Sinatra School of the Arts High School

• Leon M. Goldstein High School for the Sciences

• Maspeth High School

• Medgar Evers College Preparatory School (2)

• Park East High School

• A. Philip Randolph Campus High School

• Academy for Software Engineering

• High School of Telecommunication Arts and Technology

• Pace High School

• Pathways in Technology Early College High School 

• Urban Assembly Gateway School for Technology

• Urban Assembly Maker Academy (2)

• Urban Assembly NY Harbor School

• Urban Assembly School for Applied Math and Science (2)

• Urban Assembly School for Criminal Justice

• Wadleigh Secondary School for the Performing & Visual Arts

• Washington Heights Expeditionary Learning School (2)

• Inwood Early College for Health and Information Technology

• Mott Hall Bronx High School

• Repertory Company High School for Theatre Arts

The Williamsburg High School of Art and Technology

BEAM students also received admissions offers from the following Specialized High Schools:

• Brooklyn Latin (4)

• Brooklyn Technical High School (2)

• High School for Math, Science and Engineering at City College (2)

• Queens High School for the Sciences at York College

• Stuyvesant

Students admitted to Specialized High Schools will choose between these schools and other admissions offers they received.

We are incredibly proud of our students!

Abay was admitted to Bard High School Early College (BHSEC) Queens.

Sarah was admitted to Manhattan Center For Science and Mathematics.

Zhixing was admitted to Brooklyn Technical High School.

Nathaniel was admitted to Park East High School.

Emma was admitted to The Brooklyn Latin School.

Jason was admitted to Aviation Career & Technical Education High School.

Adrianna (Adri) was admitted to Bedford Academy High School.

**We say to date because every year a few BEAM students are under-matched in this process. We are currently working with students who were not admitted to high schools that meet our standards to make sure that they can navigate the appeals process and find a good fit for the next four years.

Got a few minutes and want to learn more about NYC high school admissions? Read this New York Times article about how game theory helped improve New York City’s high school application process.

Let's celebrate 𝜋!

Above: The first 54 digits of 𝜋 represented by colored discs. Design inspired by Martin Krzywinski’s 2013 Pi poster featured in the Numberphile video “Pi is Beautiful.”

Happy 𝜋 day! 𝜋 is probably the most familiar of the irrational numbers, and it represents a truly amazing mathematical fact: no matter what size circle you take, if you divide its circumference by its diameter, you always get the same number! That number, 𝜋, can be approximated as a fraction, such as 22/7, or a decimal, 3.14159…

The image above is actually another way to represent 𝜋. Instead of using digits, this image encodes 𝜋 in colors, where each of the numerals from 0 - 9 is matched to a different color.

A digit in the sequence of 𝜋 is then represented by a shaded disc, where the outside is the color corresponding to the digit itself, and the inside is the color of the digit that follows two decimal places later. The discs spiral from the outside to the inside, starting from the top left and moving right. The drawing represents a rich tradition of finding surprising beauty in mathematical randomness. The visualization was inspired by the work of Martin Krzywinski, which is featured in Numberphile’s video “Pi is Beautiful.”

It would be easy to overlook the richness and beauty embedded in 𝜋. The same thing can happen with math and mathiness. Sometimes, we’re quick to pigeonhole others and ourselves into convenient categories of math people or non-math people. It’s easy to decide what math should look like, or make assumptions about who looks like a mathematician and who doesn’t.

This 𝜋 day let’s take a step back from our preconceived notions. Celebrate the beauty and complexity of pi and of math, and remember that there's beauty and complexity in who is and who can be a mathematician, as well!

And if you’d like to celebrate 𝜋 Day with a little extra math, try out the challenge problem below. (The answer appears after the problem.) 

---

Challenge problem: Jarek is bored in class and starts putting numbers on his paper like in the following pattern:

If he's really bored and keeps going with this pattern for a long time, what are the 8 numbers that will surround the square containing 1,000,000?

Bonus: What are the eight numbers surrounding the square containing 1,000,010?

---

Solution:

The numbers arrange themselves in squares. For example, 4 is in the top-left of a square containing the numbers 1-4, while 16 is in the top-left of a square containing 1-16, etc. There is a pattern of even square numbers going up and to the left, so because 1,000,000=1000^2, it is in the top left of a square containing the numbers 1-1,000,000.

That means that directly to the right of it, there will be the number 999,999, and directly to the left will be the number 1,000,001. That is when the pattern turns down, so below that is 1,000,002 (which is down-left from 1,000,000). So we've found three of the numbers around 1,000,000.

Down and to the right of 1,000,000, there will be the number 998^2=996,004 because another square finishes there. To the left of that (and right below 1,000,000) is 996,005.

Up and to the left of 1,000,000 is 1002^2=1,004,004. To the right of that (and directly above 1,000,000) is 1,004,003. To the right of that (and above-right of 1,000,000) is 1,004,002.

Thus, the eight numbers near 1,000,000 are 996,004, 996,005, 1,000,002, 999,999, 1,000,001, 1,004,002, 1,004,003, and 1,004,004.

Now, for the extra bonus. The number 1,000,010 appears nine spaces below 1,000,001 along the side of the square. Directly to the right of it is the number that is eight spaces below 996,005, which is 996,013. Directly to the left of it is the number that is ten spaces below 1,004,005, which is 1,004,015.

Above and below 1,000,010 are 1,000,009 and 1,000,011. Above and below 996,013 are 996,012 and 996,014. Above and below 1,004,015 are 1,004,014 and 1,004,016.

Thus, the eight numbers near 1,000,010 are 996,014, 1,000,011, 1,004,016, 996,013, 1,004,015, 996,012, 1,000,009, and 1,004,014.